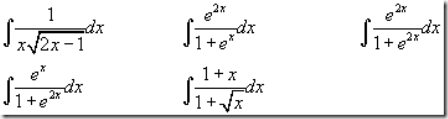
Antes de comenzar el nuevo tema hemos resuelto algunas dudas que habéis encontrado al hacer las relaciones:
Después hemos comenzado el nuevo tema: La integral definida. Hoy hemos explicado el concepto de área. Aquí os dejo una explicación mucho más rigurosa, extraída de la página http://thales.cica.es/ En este curso no se exige esta rigurosidad, pero considero que es fundamental para un alumno que se dispone a cursar estudios universitarios entrar en contacto con la forma en que se van a trabajar las matemáticas el curso próximo.
En geometría elemental se deducen fórmulas para las área de muchas figuras planas, pero un poco de reflexión hace ver que raramente se da una definición aceptable de área, el área de una región se define a veces como el número de cuadrados de lado unidad que caben en una región, pero por ejemplo el círculo de radio unidad tiene por área el número irracional  pero no está claro cual es el significado de
pero no está claro cual es el significado de  cuadrados.
cuadrados.
En general se tiene la percepción intuitiva de que una región contenida dentro de una curva cerrada posee un "área" la cual mide el número de unidades cuadradas dentro de la curva. Las propiedades básicas del área que la intuición sugiere son:
-
El área es un número (positivo, dependiente de la elección de la unidad de longitud.
-
Este número es el mismo para figuras congruentes.
-
Para todos los rectángulos es el producto de las longitudes de los lados adyacentes.
-
Para una región descompuesta en secciones el área total es igual a la suma de las áreas de las secciones..
Una consecuencia inmediata es el hecho de que: para una región A que es parte de una región B el área de A no puede ser mayor que el área de B.
Estas propiedades permiten el cálculo directo del área de cualquier figura que pueda ser descompuesta en un número finito de rectángulos. Más generalmente para asignar un valor S al área de una región R (zona azul y roja) consideramos otras dos regiones R’ (inscrita zona azul)) y R’’ (circunscrita, zona azul más roja más amarilla) de áreas S’ y S’’ respectivamente y que se pueden descomponer en rectángulos donde R’’ contiene a R y R’ está contenido en R . Se sabe al menos que S’<S<S’’. El valor de S quedará completamente determinado si se encuentran sucesiones de regiones circunscritas  y regiones inscritas
y regiones inscritas  que puedan ambas descomponerse en rectángulos y tales que las áreas
que puedan ambas descomponerse en rectángulos y tales que las áreas  y
y  tengan el mismo límite cuando n tiende a infinito. Esto es remontándonos a la antigüedad, el método de exhaución y el cual es usado en geometría elemental para el área de un circulo. La formulación precisa de esta idea, nos conduce ahora a la noción de integral.
tengan el mismo límite cuando n tiende a infinito. Esto es remontándonos a la antigüedad, el método de exhaución y el cual es usado en geometría elemental para el área de un circulo. La formulación precisa de esta idea, nos conduce ahora a la noción de integral.

La noción analítica de integral surge cuando se asocian áreas con funciones: considérese el área de una región acotada por el eje horizontal, las rectas x =a , x = b y la gráfica de la función f tal que  para todo x de [a,b]. Estas regiones las denotamos por R(f, a, b) e incluyen rectángulos (figura 2)
para todo x de [a,b]. Estas regiones las denotamos por R(f, a, b) e incluyen rectángulos (figura 2)

El número que asignamos como área de R(f, a, b) lo llamamos eventualmente integral de f

sobre [a,b]. En realidad la integral se define también para funciones que no satisfacen la condición  para todo x de [a,b]. Si f es la función dibujada en la figura 3, la integral representará la diferencia entre las áreas de las regiones sombreadas en azul claro y de sombreado en amarillo (área "algebraica" de R(f, a, b))
para todo x de [a,b]. Si f es la función dibujada en la figura 3, la integral representará la diferencia entre las áreas de las regiones sombreadas en azul claro y de sombreado en amarillo (área "algebraica" de R(f, a, b))
La idea que ampara la definición que vamos a dar se indica en la figura 4. El intervalo [a,b] se ha dividido en cuatro subintervalos [t0 , t1] [t1 , t2] [t2 , t3] [t3 , t4] por medio de los números t0 , t1 , t2 , t3 , t4 con a = t0 < t1 < t2 < t3 < t4 = b (la numeración empieza por 0 de modo que subíndice más grande indica el número de subintervalos).
Sobre el primer intervalo [t0 , t1] la función f tiene el valor mínimo m1 y el valor máximo M1; análogamente, sea mi el valor mínimo y Mi el valor máximo de f sobre el intervalo i-ésimo [ti-1 , ti]. La suma  representa el área total de los rectángulo que quedan dentro de la región R(f, a, b) (los coloreados de azul), mientras que la suma:
representa el área total de los rectángulo que quedan dentro de la región R(f, a, b) (los coloreados de azul), mientras que la suma:

representa el área total de los rectángulo que contienen a la región R(f, a, b) (rectángulos de color azul más rojo). El principio que nos va a guiar en nuestro intento de definir el área de A R(f, a, b) será la observación de que A debe satisfacer  y que esto debe ser verdad, cualquiera que sea la división que se haga del intervalo [a, b]. es de esperar que determinen A
y que esto debe ser verdad, cualquiera que sea la división que se haga del intervalo [a, b]. es de esperar que determinen A

DEFINICIÓN DE PARTICIÓN:
Sea a<b. recibe el nombre de partición del intervalo [a, b] todo conjunto finito de puntos {t0 , t1 , t2 , ........tn-1 , tn} de [a, b] de forma que uno de ellos coincide con a y otro con b, a = t0 < t1 < ......... < tn-1 < tn = b
DEFINICIÓN DE SUMA INFERIOR Y SUPERIOR:
Sea f una función acotada en el intervalo [a , b] y P = {t0 , t1 , t2 , ....... tn} una partición del intervalo [a , b]. Sea  y
y 
Se define la suma inferior de f para P como:

Se define la suma superior de f para P como:

Las sumas inferiores y superiores se corresponden con las sumas s y S, respectivamente, del ejemplo anterior; se supone que representan las totales de los rectángulo que quedan por debajo y por encima de la gráfica de f., no obstante estas sumas han sido definidas sin recurrir al concepto de área.
Hay que tener en cuenta dos cosas:
-
La condición de que f esté acotada en el intervalo [a , b] es fundamental para que los mi y Mi queden definidos.
-
Los mi y Mi han sido definidos como ínfimos y supremos, y no como mínimos y máximos, ya que no se le ha exigido a f que sea continua.
Evidentemente si P una partición cualquiera  pues por la forman en que están definidas cada una de ellas se tiene que
pues por la forman en que están definidas cada una de ellas se tiene que  .
.
Lo que ya no es tan evidente es que si P1 y P2 son dos particiones cualesquiera de [a,b] se cumpla:  ya que debería de cumplirse
ya que debería de cumplirse  . A continuación trataremos de demostrar que
. A continuación trataremos de demostrar que  basándonos en el comportamiento de las sumas inferiores y superiores al añadir más puntos a una partición. En la figura 5 la partición P contiene los puntos de color rojo y la partición Q contiene los puntos de color rojo y los puntos de color verde. Según esta figura los rectángulos de la partición Q (color azul más amarillo) constituyen una aproximación mejor a la región R(f, a, b) que los correspondientes a la partición P (rectángulos de color azul).
basándonos en el comportamiento de las sumas inferiores y superiores al añadir más puntos a una partición. En la figura 5 la partición P contiene los puntos de color rojo y la partición Q contiene los puntos de color rojo y los puntos de color verde. Según esta figura los rectángulos de la partición Q (color azul más amarillo) constituyen una aproximación mejor a la región R(f, a, b) que los correspondientes a la partición P (rectángulos de color azul).

En consecuencia podremos enunciar el siguiente.
LEMA:
Si la partición Q contiene a la partición P (es decir todos los puntos de P están en Q), entonces:

DEMOSTRACIÓN:
Consideremos primeramente el caso especial en el que la partición Q contiene exactamente un punto más que la P (figura 6)

 siendo
siendo

Sea 

Tenemos que 



Sean los conjuntos 
y teniendo en cuenta que necesariamente se tiene que
necesariamente se tiene que  de la misma forma
de la misma forma  por lo tanto de estas desigualdades, y tendiendo en cuenta que
por lo tanto de estas desigualdades, y tendiendo en cuenta que solamente se diferencian en los sumandos:
solamente se diferencian en los sumandos:
mk(tk - tk-1) y m’(u - tk-1) + m’’(tk - u),
 (pues
(pues  ) lo que demuestra que
) lo que demuestra que  .
.
Análogamente las sumas superiores  solamente se diferencia en el sumando Mk(tk - tk-1) y
solamente se diferencia en el sumando Mk(tk - tk-1) y  y como
y como  se tiene que:
se tiene que:  , por lo tanto
, por lo tanto 
En el caso general de que Q contiene a P, la partición Q puede obtenerse fácilmente de la P añadiendo un punto cada vez y obtenido así una sucesión de particiones P = P1, P2 ,.......Pn = Q en la que Pk contiene exactamente un punto mas que Pk-1 por lo tanto:


C.C.Q.D.
TEOREMA 1:
Sean P1 y P2 dos particiones del intervalo [a , b], y sea f una función acotada sobre [a,b]. entonces:

DEMOSTRACIÓN:
Tomemos un partición P de [a , b] que contenga a la vez a P1 y P2, podría ser  Como consecuencia del lema anterior al contener P todos los puntos de P1 y P2 se tiene que:
Como consecuencia del lema anterior al contener P todos los puntos de P1 y P2 se tiene que:
 C.C.Q.D.
C.C.Q.D.
Por P [a , b] denotamos el conjunto de todas las particiones de [a , b]
Como esto es válido para toda partición de [a , b] se tiene que cualquier suma superior es cota superior del conjunto  , por lo tanto:
, por lo tanto:
 para toda partición P’, en consecuencia
para toda partición P’, en consecuencia  es una cota inferior del conjunto de todas las sumas superiores de f por lo tanto
es una cota inferior del conjunto de todas las sumas superiores de f por lo tanto  .
.
Está claro que:

y

para cualquier partición P’
Puede ocurrir que

en cuyo caso este sería el único número comprendido entre la suma inferior y la suma superior de f para todas las particiones y este número podría se ideal para el área de R(f, a, b). Pero por el contrario si  entonces todo número x comprendido entres ellos verifica
entonces todo número x comprendido entres ellos verifica  para todas las particiones P’.
para todas las particiones P’.
Los dos ejemplos siguientes ponen de manifiesto que son posibles los dos casos:
EJEMPLO 1: Sea f(x) = c  y P = {t0 , t1 ,......, tn} una partición del intervalo [a , b], entonces c = mi = Mi y se tiene:
y P = {t0 , t1 ,......, tn} una partición del intervalo [a , b], entonces c = mi = Mi y se tiene:

por lo tanto en este caso 
EJEMPLO 2: Consideremos ahora la función f definida por:

Si P = {t0 , t1 ,......, tn} es una partición cualquiera, entonces mi = 0 pues en [ti-1 , ti] hay algún irracional y Mi = 1 pues en [ti-1 , ti] hay algún racional. Por lo tanto se tiene que:

Por lo tanto en este caso tenemos que:

y según esto cualquier número comprendido entre 0 y b - a podría ir igual de bien para el área de R(f, a, b) por lo que se estás justificado no asignarle área alguno. De hecho, cuando no se le asignará área a la región.
no se le asignará área a la región.
DEFINICIÓN DE FUNCIÓN INTEGRABLE:
Una función f acotada sobre [a, b] es integrable sobre [a, b] cuando se verifique:

A este número se le llama integral de f sobre [a, b] y se denota por 
(El símbolo  recibe el nombre de signo integral en su origen era una s alargada, por "suma"; los números a y b reciben el nombre de limites de integración inferior y superior). La integra
recibe el nombre de signo integral en su origen era una s alargada, por "suma"; los números a y b reciben el nombre de limites de integración inferior y superior). La integra  recibe el nombre de área de R(f, a, b) cuando
recibe el nombre de área de R(f, a, b) cuando  para todo x de [a, b]
para todo x de [a, b]
Según la definición si f es integrable  . Además
. Además  es el único número que cumple esta propiedad.
es el único número que cumple esta propiedad.
Esta definición prepara, pero no resuelve, el problema planteado: no sabemos cuáles funciones son integrables (ni tampoco sabemos cómo hallar la integral de f sobre [a , b] cuando f es integrable).
TEOREMA 2:
Si f es una función acotada sobre [a , b], se tiene que f es integrable sobre [a , b] si y sólo si, pata todo  existe una partición P de [a , b] tal que:
existe una partición P de [a , b] tal que:

DEMOSTRACIÓN:
Supongamos en primer lugar que para todo  existe un partición P de forma que
existe un partición P de forma que teniendo en cuenta que para cualquier partición P se tiene que
teniendo en cuenta que para cualquier partición P se tiene que  y
y  tendremos que:
tendremos que:
 y como esto es válido para cualquier
y como esto es válido para cualquier  positivo se deduce que
positivo se deduce que  luego f es integrable.
luego f es integrable.
Recíprocamente, supongamos ahora que f es integrable, luego  , sea un
, sea un  positivo cualquiera, entonces existirán al menos dos particiones P1 y P2 tales que:
positivo cualquiera, entonces existirán al menos dos particiones P1 y P2 tales que:


Sumando estas dos expresiones y tendiendo en cuenta que  se tiene que
se tiene que  . Consideremos ahora la partición
. Consideremos ahora la partición  se tendrá que:
se tendrá que:
 , de donde se deduce:
, de donde se deduce:
 .
.
Con lo que queda demostrado que para todo  positivo existe puna partición P tal que
positivo existe puna partición P tal que 
C.C.Q.D.
En realidad este teorema equivale solamente a expresar de otro modo la definición de integrabilidad, pero tal vez sea una expresión más sencilla, pues en ella no intervienen el supremo ni el ínfimo que no siempre son fáciles de manejar.
no puede tener más de una raíz en el intervalo [-1,1], cualquiera que sea el valor de b. Enuncia los teoremas que uses e intenta ser lo más riguroso posible en la explicación. [Observa que no te pido que demuestres que tiene solución, sino que si tiene, no puede tener más de una]
se traza una cuerda que une los puntos de la parábola de abcisas x=1 y x=3. Halla la ecuación de la recta tangente a la parábola que es paralela a esa cuerda. Dibuja el ejercicio.

. En caso afirmativo, obtén el valor donde se cumple la tesis.
un polinomio. Halla a,b y c para que la función corte al eje de abcisas en x=-1 y tenga un punto de inflexión en (2,1)