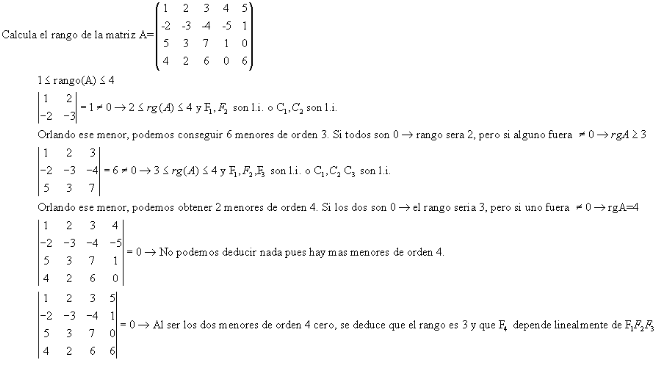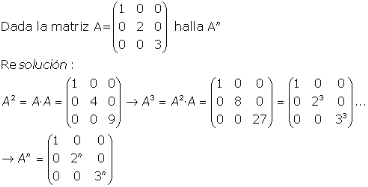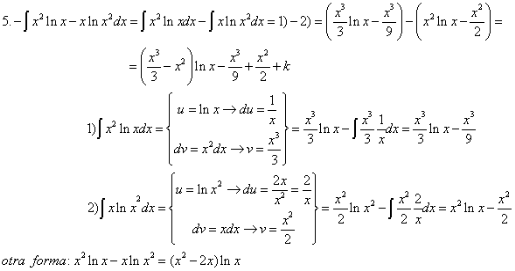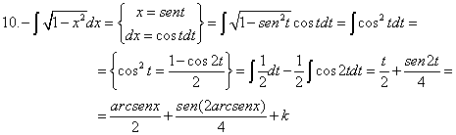Hoy he explicado el concepto de rango de una matriz, concepto básico para el estudio y discusión de sistemas de ecuaciones lineales.
jueves, 26 de marzo de 2009
miércoles, 25 de marzo de 2009
Diario de clases: Miércoles 25 de Marzo de 2009
Hoy hemos trabajado los determinantes de orden superior a 3. Hemos comenzado definiendo los siguientes conceptos:
Si los elementos de una fila o columna de una matriz cuadrada se multiplican por sus respectivos adjuntos y se suman los resultados, se obtiene el determinante de la matriz inicial. Se dice entonces que el determinante está desarrollado por los elementos de esa fila o columna.
Hemos realizado en clase los siguientes ejercicios:
martes, 24 de marzo de 2009
Diario de Clases: Martes 24 de Marzo de 2009
En la clase de hoy hemos seguido trabajando las propiedades de los determinantes:
- El determinante de una matriz es un número.
- El determinante de una matriz coincide con el de su traspuesta.
- Si un determinante tiene una línea (fila o columna) de ceros, el valor del determinante es 0.
- Si permutamos dos filas o dos columnas, el determinante cambia de signo.
- Si un determinante tiene dos filas (o dos columnas) iguales o proporcionales su valor es 0.
- Podemos sacar factor común de una fila (o de una columna). Esta propiedad la tendemos a confundir con la propiedad de sacar factor común en matrices. Recordad que para sacar factor común en matrices se debe hacer de todos los elementos de la matriz. En determinantes se saca factor común de filas o de columnas. Aquí os dejo un ejercicio aclaratorio:
- El determinante de la suma de dos matrices no es la suma de sus determinantes. |A+B|><|A|+|B|. Un determinante puede descomponerse en suma de dos del siguiente modo:
- Si a una fila (o a una columna) se le suma otra fila (u otra columna) multiplicada por un número, el determinante no cambia de valor.
- El determinante del producto de dos matrices es igual al producto de sus determinantes: |A·B|=|A|·|B|
Ejercicios hechos en clase:
Mañana trabajaremos los determinantes de orden superior a tres, definiendo para ello los conceptos de menor complementario y de adjunto de un elemento de una matriz.
lunes, 23 de marzo de 2009
Diario de clases: Lunes 23 de Marzo de 2009
Hoy hemos repasado la definición de determinante y hemos trabajado las propiedades:





martes, 17 de marzo de 2009
Diario de Clases: Martes 17 de Marzo de 2009
Para comenzar, hemos resuelto posibles dudas de lo “explicado” el pasado jueves 12 de marzo. Después hemos comenzado a explicar el concepto de matriz inversa.

lunes, 16 de marzo de 2009
Diario de Clases: Lunes 16 de Marzo de 2009


Os he dejado una relación de ejercicios de repaso de las operaciones básicas con matrices estudiadas hasta ahora.
domingo, 15 de marzo de 2009
World Builder by Bruce Branit
Diario de clases: Jueves 12 de Marzo de 2009
Hoy está convocada una nueva jornada de huelga de estudiantes y no ha asistido ningún alumno a clase. Aquí os dejo lo que tenía programado dar hoy.
Matriz traspuesta, propiedades. Matriz simétrica y antisimétrica

Diario de Clases: Miércoles 11 de Marzo de 2009
Hoy hemos trabajado el producto y potencias de matrices:
Hemos realizado varios ejercicios básicos de multiplicación de matrices, recalcando que el producto no cumple la propiedad conmutativa.
Diario de Clases: Martes 10 de Marzo de 2009
En el día de hoy hemos realizado la segunda parte del examen Final del Bloque II. Aquí os dejo la versión imprimible
Ejercicio 1.- (1’5 pto) El área del recinto limitado por las curvas de ecuaciones e
con a>0, vale 3. Calcula el valor de a
Ejercicio 2.- (1’5 pto) Considere la función definida por . Dibuja el recinto limitado por la gráfica de f, la recta tangente a f en el punto x=1 y el eje OX. Calcula su área.
Ejercicio 3.- (1’5 pto) Consideremos las funciones Esboza las gráficas de f y de g calculando sus puntos de corte. Calcula el área de cada uno de los dos recintos limitados entre las gráficas de f y de g.
Ejercicio 4.- (1’5 pto) Dada la función Halla los máximos y mínimos y los valores que alcanzan.
Ejercicio 5.- (1’5pto) Representa gráficamente la función y calcula el volumen del cuerpo de revolución engendrado al girar alrededor del eje X la curva.
lunes, 9 de marzo de 2009
Diario de clases: Lunes 9 de Marzo de 2009
Tal y como teníamos previsto, hoy hemos realizado la primera parte del Examen Final del Bloque II Análisis Matemático II. Aquí os dejo la versión imprimible.
Corrección del examen: