Diario de Clases: Jueves 29 de Enero de 2009

   Hoy se ha realizado el examen de recuperación del Bloque I. Aquí tenéis el examen. También os  podéis bajar aquí la versión imprimible.

Ejercicio 1.- (1,25 ptos) Las siguientes gráficas se corresponden con f’ (x) y f’’(x) . Identifícalas y estudia, a partir de las gráficas, la continuidad, derivabilidad, crecimiento y decrecimientos, máximos, mínimos, puntos de inflexión, concavidad y convexidad de la función f. A partir de lo estudiado, haz un esbozo de la gráfica de la función f sabiendo que los puntos de corte con los ejes son (-2’58 , 0), (0 , 0) y (2’58 , 0)

Ejercicio 2.- (1,25 ptos) Demuestra que la ecuación no puede tener más de una raíz en el intervalo [-1,1], cualquiera que sea el valor de b. Enuncia los teoremas que uses e intenta ser lo más riguroso posible en la explicación. [Observa que no te pido que demuestres que tiene solución, sino que si tiene, no puede tener más de una]

Ejercicio 3.- (1,25 ptos) Dada la parábola se traza una cuerda que une los puntos de la parábola de abcisas x=1 y x=3. Halla la ecuación de la recta tangente a la parábola que es paralela a esa cuerda. Dibuja el ejercicio.

Ejercicio 4.- (1,25 ptos) Resuelve dos de los siguientes límites:

Ejercicio 5.- (1,25 ptos) Comprueba si la función verifica las condiciones del teorema de Rolle en el intervalo . En caso afirmativo, obtén el valor donde se cumple la tesis.

Ejercicio 6.- (1,25 ptos) Sea un polinomio. Halla a,b y c para que la función corte al eje de abcisas en x=-1 y tenga un punto de inflexión en (2,1)

Ejercicio 7.- (1,25 ptos) Un nadador A se encuentra a 3 km de la playa enfrente de una caseta. Desea ir a B en la misma playa, a 6 km de la caseta. Sabiendo que nada a 3km/hora y anda por la arena a 5 km/hora, averigua a qué lugar debe dirigirse a nado para llegar a B en el menor tiempo posible:

Ejercicio 8.- (1,25 ptos) Sea f la función definida por

a) Determina el dominio de definición, los puntos de corte con los ejes coordenados y las posibles simetrías.

b) Estudia las asíntotas de la gráfica de f

c) Determina los intervalos de crecimiento y de decrecimiento y los extremos relativos de f (puntos donde se obtienen y valores que se alcanzan)

d) Estudia la existencia de puntos de inflexión y la curvatura de la función

e) Esboza la gráfica de f

Ejercicio VOLUNTARIO.- (A LA PUNTUACIÓN OBTENIDA EN LOS DEMÁS EJERCICIOS SE LE SUMARÁ LO OBTENIDO EN ESTE EJERCICIO)

Explica razonadamente:

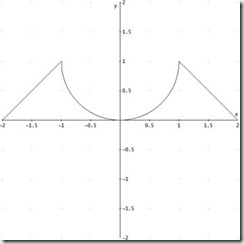
a) De la función f(x) definida en [-2,2], se conoce su gráfica, dada por:

i. (0,5 ptos) Dibuja razonadamente la gráfica de f´(x)

ii. (0,5 ptos) Dibuja razonadamente la gráfica de f ‘’(x)