Diario de clases: Martes 29 de Septiembre de 2009

También hemos trabajado el problema de la cuadratura del círculo que planteamos ayer, introduciendo los otros dos problemas clásicos de la geometría griega, la trisección del ángulo y la duplicación del cubo. Aquí os dejo una lectura, que por su interés, sería conveniente que leáis con atención, sobre todo los que estais matriculados en la asignatura Dibujo Técnico II.

Geometría con regla y compás.

Entre los griegos se consideraba que la forma correcta de resolver los problemas geométricos (ellos no usaban ecuaciones como nosotros: aún no había nacido Descartes) era utilizando únicamente dos intrumentos: la regla (sin graduar) y el compás.

La culpa es muy posible que sea de Platón, pues consideraba “por alguna mística razón solo conocida por él y su Dios geómetra” que resolver los problemas geométricos por medios mecánicos, es decir, cualquier otro que no fuese la regla y el compás, era vulgar y degradante. Así lo cuenta Plutarco en sus Vidas paralelas: “...Platón se indispuso e indignó contra ellos [Eudoxo y Arquitas], porque degradaban y echaban a perder lo más excelente de la geometría con trasladarse de lo incorpóreo e intelectual a lo sensible y emplearla en los cuerpos que son objeto de oficios toscos y manuales...”.

Uno puede pensar que esta obsesión de Platón por la regla y el compás era un puro capricho, y puede que acierte: posiblemente fue a causa del valor casi divino que daba a las ideas por lo que concedió especial importancia a unos objetos con una simetría tan perfecta como son rectas y circunferencias. Además, todo hay que decirlo, también debió influir cierto aristocrático desprecio por su parte hacia todo lo que sonase a oficio artesano.

Sin embargo, por aquel entonces el platonismo no era la única forma de pensar. La escuela de Demócrito había introducido el atomismo en geometría de tal modo que consideraban los segmentos, las superficies y volúmenes constituidos por una cantidad finita de átomos. Resulta que este método, aunque poco riguroso, permitía encontrar fácilmente nuevos resultados, y un futuro esplendoroso se abría para la geometría.

Pero no fueron por ahí los tiros. Los pensadores griegos se encontraron con dos métodos a su disposición: uno riguroso, pero estéril, y otro, el atomista, informal pero fértil. ¿Quién ganó? Pues fue el idealismo platónico el que venció al materialismo atomista, lo cual solo se explica si pensamos que las matemáticas griegas fueron el producto de una clase ociosa basada en la esclavitud y más interesada en la contemplación que en la invención: ¿para qué cambiar el mundo si a ellos les iba de miedo?

En fin, que armados con tan corto arsenal los griegos se lanzaron al estudio de la geometría. Y no les fue tan mal, aunque en su camino se encontraron con tres problemas que fueron incapaces de resolver: la cuadratura del círculo, la duplicación del cubo y la trisección del ángulo. La razón solo se supo dos mil años después: eran irresolubles.

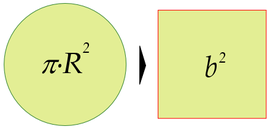
Y lo cierto es que nada en su descripción hace sospechar grandes dificultades: la cuadratura del círculo trata de construir un cuadrado con la misma superficie que un círculo dado, mientras que la trisección del ángulo busca dividir un ángulo dado en tres ángulos iguales. La duplicación del cubo tiene su propia leyenda: en tiempos de Pericles una epidemia de peste estaba diezmando la población. Los atenienses mandaron una delegación al oráculo de Delfos para preguntarle acerca de qué podían hacer para aplacar a los dioses. El Oráculo les contestó que debían duplicar en tamaño el altar cúbico dedicado a Apolo. Los griegos se pusieron a la faena y construyeron un altar cúbico con el doble de lado. Pero la peste no cesó. Y es que al doblar el lado habían multiplicado el volumen por ocho, y no es eso lo que se les pedía...

Imposibles...

Caprichos divinos aparte, lo cierto es que los problemas descritos no parecen tan difíciles, ¿verdad? Sin embargo, los griegos, que sabemos fueron excelentes geómetras, fracasaron en sus intentos de resolverlos. ¿Por qué? Pues muy sencillo: porque no se puede. Literalmente, los tres problemas describen tareas que son imposibles de realizar usando únicamente regla y compás.

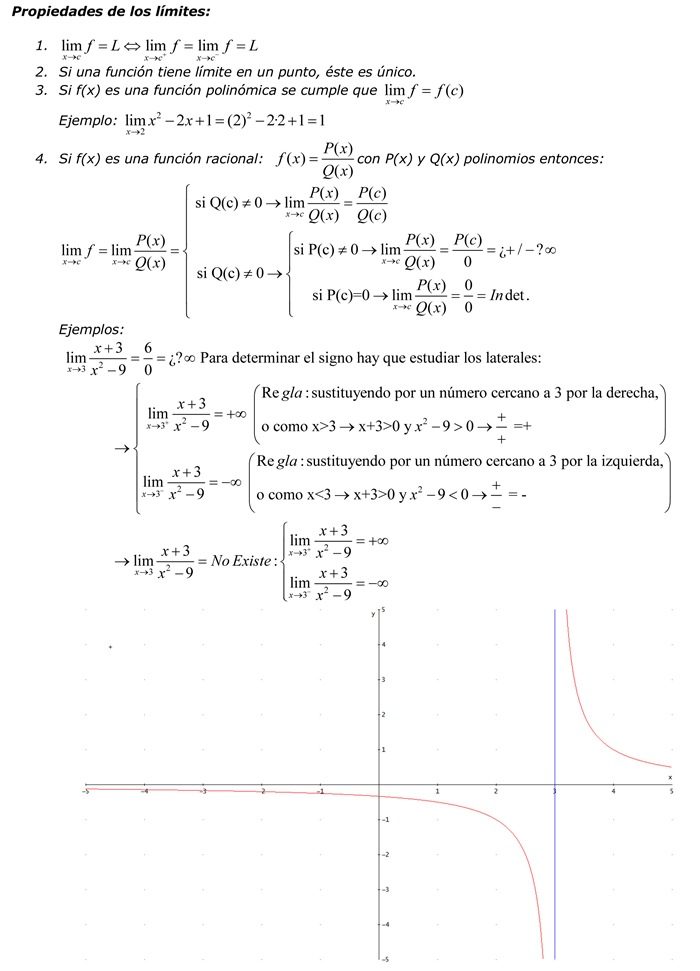
Veamos por qué: cualquier operación que realicemos con una regla es equivalente a la resolución de una ecuación de primer grado, mientras que las realizadas con un compás equivalen a resolver ecuaciones de segundo grado, lo cual es lógico, pues con la regla dibujamos rectas, objetos que se expresan mediante ecuaciones de primer grado, y con el compás circunferencias, las cuales se expresan mediante ecuaciones de segundo grado. Dicho de otro modo: con la regla y el compás podemos realizar sumas, restas, multiplicaciones, divisiones, y raíces de índice igual a una potencia de dos.

Pero resulta que la resolución de la cuadratura del círculo requiere conocer el valor del número π, que es un número trascendente (es decir, que no se puede obtener como solución de ninguna ecuación algebraica); resulta también que para trisecar el ángulo es necesario realizar raíces cúbicas, y que para duplicar el cubo necesitamos la raíz cúbica de dos. Y como el cálculo de π y de raíces cúbicas no es posible, por lo dicho anteriormente, utilizando únicamente regla y compás, nuestros tres problemas se quedan sin solución.

Y lo más tremendo es que alguno de los resultados que justifican la imposibilidad de estos problemas, como por ejemplo la trascendencia de π, solo se obtuvieron veintitantos siglos después de que se planteasen.

...aunque no tanto

¿Quiere decirse entonces que no podemos resolver unos problemas en apariencia tan sencillos? No: los tres famosos problemas de la geometría griega solo son irresolubles si nos limitamos a la regla sin graduar y al compás. Pero las dificultades se desvanecen cuando podemos utilizar otro tipo de curvas o hacer marcas sobre nuestra regla. De hecho, no todos los griegos se plegaron a dicha limitación, y fueron capaces de resolver los problemas de marras utilizando nuevas y sorprendentes curvas, de las que a continuación doy algunos ejemplos:

• La espiral de Arquímedes: es el lugar geométrico descrito por un punto que se desplaza a lo largo de una semirrecta con velocidad uniforme al tiempo que esta gira, también uniformemente. El mismo Arquímedes la atribuye a su amigo Conon de Alejandría. Con ella se resuelve la trisección del ángulo y la cuadratura del círculo.
• La trisectriz de Hipias: curva inventada por Hipias de Ellis. Permite la duplicación del cubo y la trisección del ángulo.
• Las cónicas: quizá el descubrimiento más importante relacionado con los tres problemas sea el que realizó Menecmo intentando conseguir la duplicación del cubo: las cónicas, curvas que resultan de cortar un cono mediante un plano y que por su importancia merecen su propia historia.

¿Entonces?

Si ya los griegos los resolvieron, ¿dónde reside la importancia de estos tres problemas? Pues reside precisamente en que, gracias a la limitación de la regla y el compás, los matemáticos se han visto obligados a investigar nuevos campos en busca de nuevas herramientas que los resolviesen o de más profundas teorías que explicasen su imposibilidad. Y es que no hay nada como las dificultades para aguzar el ingenio.

De todas formas, no todo han sido aciertos: la aparente sencillez de la cuadratura del círculo ha obsesionado durante siglos a grandes y pequeñas mentes y dado lugar a todo tipo de extravagancias (ver como ejemplo el caso Hobbes). Por eso dijo Underwood Dudley que "Uno de los inesperados efectos beneficiosos de la televisión es que la gente ahora la ve en vez de producir panfletos cuadrando el círculo."

Aunque, la verdad, yo preferiría que el personal siguiese con los panfletos.

Para terminar, una curiosidad: la duplicación del hipercubo tetradimensional podría hacerse con regla y compás, pues en cuatro dimensiones lo que hace falta no es la raíz cúbica de dos, sino la raíz cuarta.

Fuente: http://www.epsilones.com/paginas/t-historias1.html

Por cierto, observad el escudo de nuestro departamento de Matemáticas, aparece un compás.

Aquí os dejo los apuntes en formato PDF

Diario de clases: Lunes 28 de Septiembre de 2009

Hoy D. Pedro Pitarch escribe un artículo de opinión en el diario ABC titulado: “Afganistan o la cuadratura del círculo”. No es mi intención entrar en detalles sobre el artículo, sólo me quedo con el título. ¿Cuadratura del círculo?. Nadie en la clase conocía su significado, así que os he propuesto un pequeño “trabajo de investigación” sobre dicho problema clásico.

¿ ?

Cuidado con “las fuentes” de las que os vais a nutrir, la web está llena de información errónea o poco precisa. En 1882, el matemático alemán Ferdinan Lindermann demostró rigurosamente que es irresoluble,  pero siempre hay alguien que se atreve a dar alguna solución. Os dejo dos enlaces, uno en el que te dan un “procedimiento” para cuadrar un círculo, y otro en el que aceptan que es irresoluble, pero te lo aproximan.

Como siempre, aquí os dejo los apuntes en formato PDF.

Diario de clases: Viernes 25 de Septiembre de 2009

Navegando en la web, he encontrado este video en el que se explica, paso a paso, un límite del tipo e, aunque es cuando x tiende a un punto. La técnica es la misma. Espero que os ayude:

http://www.cibermatex.com/spip.php?article42

Aquí os dejo los apunte en formato PDF

El próximo día seguiremos trabajando esta indeterminación, y comenzaremos el estudio de los límites en un punto.

Diario de clases: Jueves 24 de Septiembre de 2009

 

En estas páginas podréis encontrar recursos on-line

enlace 1

enlace 2

 Aquí os dejo los apuntes en formato PDF

Diario de Clases: Martes 21 de Septiembre de 2009

 

Aquí os dejo los apuntes en formato PDF

Documento de Orientación

Espero que todos vosotros podais presentaros a la Prueba de Acceso a la Universidad el próximo mes de Junio. Acaba de publicarse el documento de orientación por el que se regirá la prueba de Matemáticas II. Es conveniente que lo leais, pues vienen estructurados los contenidos mínimos que debeis alcanzar este curso y un modelo de examen. Aquí os dejo el enlace.

También se han publicado los documentos de orientación del resto de las asignaturas. En esta página los podreis consultar todos.

Diario de clases: Lunes 21 de Septiembre de 2009

Tras repasar lo estudiado la semana pasada, hemos seguido trabajando las operaciones en las que interviene el infinito:

En algunos casos no se puede determinar si un límite existe y cuál es su resultado. Estos casos se denominan indeterminaciones:

Diario de clases: Viernes 18 de Septiembre de 2009

INTRODUCCIÓN HISTÓRICA AL ANÁLISIS MATEMÁTICO

Uno de los pilares básicos sobre los que se cimienta el gran edificio de las Matemáticas es el concepto de función. Las funciones, además de ser un importante instrumento dentro de las Matemáticas, también lo son en las demás ciencias: Física, Astronomía, Biología, Economía, Sociología, Medicina, etc.

Cuando iniciamos un estudio en el campo científico, uno de los objetivos es obtener un modelo matemático que nos permita entender y expresar como se relacionan las distintas magnitudes que intervienen. Dicho modelo se debe ajustar a las observaciones o datos empíricos obtenidos.

Se puede afirmar que la culminación del proceso de elaboración del concepto de función es una de las grandes aportaciones de la ciencia en el siglo XVII. Fue un proceso lento que en realidad había comenzado ya en el siglo XIV.

La matemática de la antigüedad fue preponderantemente estática. Es cierto que la geometría de los griegos constituyó una genial exploración racional del espacio, dando origen a una concepción de la matemática y de la ciencia que en esencia es la de hoy, después de veintiséis siglos. Pero la exploración de los diversos tipos de movimientos, la introducción en la matemática de la noción de cambio en el tiempo, la cuantificación de la causalidad en la determinación de un efecto, era algo para lo que la matemática no estuvo suficiente madura, sino después de muchos siglos. De hecho se puede afirmar que durante mucho tiempo el avance en muchos frentes de la ciencia se vio frenado por la incapacidad de la matemática para aportar herramientas adecuadas.

La noción de función surge con fuerza en el campo de la ciencia debido a la generalización del uso del sistema decimal, por la posibilidad de representación y cálculo simbólico de magnitudes heredadas del álgebra y por las posibilidades de medición y observación conseguidas a través de nuevos instrumentos.

Las funciones más interesantes, por supuesto, son las funciones reales de variable real, es decir, aquellas definidas sobre los números reales cuyos valores son también números reales. Su estudio constituye el armazón de toda la matemática actual y, consecuentemente, de toda la ciencia y tecnología modernas. Estas funciones van a constituir el objetivo de este bloque.

En el desarrollo del cálculo infinitesimal, en el siglo XVII, al estudiar la derivada de funciones, la integral,... surgieron problemas relacionados con los procesos infinitos que hubo que introducir, aun sin entenderlos muy bien. Hasta finales del siglo XIX con Weierstrass, no se logró una expresión del cálculo infinitesimal suficientemente rigurosa y correcta. Ello fue posible gracias a la revisión de conceptos básicos como el número real, la noción de límite, la de continuidad, etc.

El antecedente más antiguo que conocemos de lo que hoy se entiende por función se remonta a la época mesopotámica. De este periodo se conservan diversas tablillas de arcilla en las que se recogen series de números relacionados entre sí.

No obstante el estudio de las funciones como relaciones de dependencia entre magnitudes no comenzó a abordarse de forma rigurosa hasta el siglo XVII.

Puede afirmarse que la idea de función está implícita en los trabajos de los matemáticos franceses Rene Descartes y P. de Fermat. Sin embargo hubo de esperar a la publicación en 1638 del Discurso e dimostrazioni matematiché intorno a due nuove scienze, del astrónomo y matemático italiano G. Galilei, para que los modelos funcionales se aplicaran decididamente en las ciencias experimentales, en especial al estudio de las leyes del movimiento.

El análisis es la rama de la matemática que proporciona métodos para la investigación cuantitativa de la dependencia de unas magnitudes respecto de otras, así como de los procesos de cambio que se producen entre ellas.

Esta disciplina surgió de la necesidad de una herramienta que permitiera abordar los problemas que preocupaban a la ciencia del siglo XVII, y que podemos englobar en dos grandes grupos:

El primer grupo incluye problemas físicos, en especial los relacionados con el cálculo de velocidades en un movimiento, junto a problemas geométricos de determinación de tangentes, máximos y mínimos, etc. Este conjunto de problemas condujo a una rama del análisis que recibe el nombre de cálculo diferencial.

El segundo abarca una serie de problemas físicos asociados al cálculo de espacio recorrido en un movimiento, así como problemas geométricos de obtención del área de una figura curvilínea: el llamado problema de la cuadratura. Este conjunto de problemas llevó a otra rama del análisis conocida como cálculo integral.

Reseñas históricas:

- Arquímedes de Siracusa (287- 212 a.C.) utiliza las primeras ideas infinitesimales en el cálculo de áreas.

- Galileo Galilei (1564-1642) estudió el movimiento desde un punto de vista cuantitativo, estableciendo leyes o funciones entre magnitudes.

- John Wallis (1616-1703) utilizó por primera vez en su obra Arithmetica infinitorum el símbolo de "" para representar el infinito.

- Isaac Barrow (1630-1677) preparó el camino para el descubrimiento del cálculo infinitesimal. Estudiaremos el año próximo un famoso teorema que lleva su nombre.

- Gottfried W. Liebnitz (1646-1716) publicó en 1686 en la revista Acta Eruditorum los principios básicos del Cálculo infinitesimal.

- Guillaume Francois Antoine de L'Hopital (1661-1704) publicó en 1696 un tratado de Cálculo diferencial titulado Analyse des infiniment petits, en el que figuraba la famosa regla que lleva su nombre.

- Isaac Newton (1642-1727) en 1693 publicó en su obra De Analysi los principios básicos del Cálculo Infinitesimal. Es considerado junto con Leibniz uno de los padres del Cálculo infinitesimal. La obra más importante de Newton fue Philosophie naturalis principia mathematica (Principios matemáticos de la filosofía natural).

- Leonard Euler (1707-1783) fue uno de los grandes matemáticos que contribuyó a la evolución del Análisis Matemático. Utilizó el símbolo y=f(x) para denotar a una función. En su obra Introductio in analysin infinitorum publicada en 1748 sistematizó los conocimientos de su época y dio una definición de función que presidió en el desarrollo de las matemáticas durante un siglo: "Función es cualquier expresión analítica formada con cantidades variables y con cantidades constantes"

- Bernard Bolzano (1781-1848) matemático checoslovaco muy preocupado por el rigor y la precisión en las demostraciones matemáticas, formuló el teorema que lleva su nombre en 1817.

- Agustín Louis Cauchy (1789-1857) es considerado como el matemático que fundamentó el Cálculo Infinitesimal. La obra fundamental de Cauchy fue Cours D'Analyse de L'Ecole Royale Polytechnique publicada en 1821 en donde cimienta el Cálculo infinitesimal en el concepto de límite.

- Peter Gustav Lejeune Dirichlet (1805-1859) dio la definición rigurosa de función, tal y como la conocemos hoy en día.

- Karl Weierstrass (1815-1897) fue el más destacado fundador de los principios del Análisis y de su rigurosa demostración. A menudo se habla de "rigor weierstrassiano" de una demostración.

- Julio Rey Pastor (1888-1962) ha sido considerado el matemático español más importante del siglo XX.

- Richard Dedekind (1831-1916) y Georg Cantor (1845-1918) demostraron que los números reales llenan o completan la recta, es decir, que a cada punto de la recta le corresponde un número real y viceversa.

1.- Límite de una función en el infinito

IMPORTANTE: Para completar tu formación, es conveniente que trabajes este recurso

Operaciones con Límites

Si f(x) y g(x) son dos funciones y existen sus límites, se cumple que:

Nota: En todas las expresiones anteriores aparece , queriendo decir que son validas tanto para como para

En el cálculo de límites es necesario operar con expresiones donde aparece infinito. Estas son algunas de las expresiones cuyos resultados son conocidos:

Evaluación

La asignatura de Matemáticas II la vamos a dividir en cuatro bloques temáticos:

Bloque I.- Análisis Matemático I

Bloque II.- Análisis Matemático II

Bloque III.- Algebra lineal

Bloque IV.- Geometría analítica

La evaluación se va a realizar de la siguiente forma:
- Pruebas escritas. Se realizarán dos exámenes por bloque . El primer examen se realizará a la mitad del bloque. El segundo se realizará a la finalización de éste y en él el alumno se examinará de todo el bloque. La nota del bloque será el resultado de dividir entre 3 la suma de la puntuación del primer examen con el doble del segundo. Habrá un examen- recuperación de cada bloque para aquellos alumnos que no hayan superado los objetivos del mismo. A esta prueba se podrán presentar aquellos alumnos que deseen subir nota, sin temor a poderla bajar.
- En Junio se realizará una segunda recuperación a la que se presentarán todos los alumnos con algún bloque suspenso. Al ser este examen de contenidos mínimos la nota máxima que el alumno podrá obtener será de un cinco, si la nota de examen está entre 5 y 7, un seis, si está entre 7 y 8, y un 7 si es superior a 8. No habrá limitación de número de bloques suspensos y de nota mínima.
- La nota de la convocatoria ordinaria se calculará haciendo la media aritmética de los cuatro bloques, siendo imprescindible tener los cuatro bloques aprobados. En el caso de tener algún bloque suspenso el alumno deberá presentarse a la convocatoria extraordinaria.
- En la convocatoria extraordinaria el alumno se examinará de toda la asignatura, independientemente de las partes que el alumno hubiera aprobado. Al ser este examen de contenidos mínimos la nota máxima que el alumno podrá obtener será de un cinco, si la nota de examen está entre 5 y 7, un seis, si está entre 7 y 8, y un 7 si es superior a 8.

Todos los exámenes se regirán por los siguientes criterios:
• Para la resolución de los ejercicios no será necesario utilizar calculadoras; no obstante, no se prohibirá su uso (siempre y cuando no sean programables o que tengan pantalla gráfica); sin embargo, durante el examen no se permitirá el préstamo de calculadoras entre estudiantes. En cualquier caso, se advierte que todos los procesos que conduzcan a la obtención de resultados deben estar suficientemente razonados.
• En los ejercicios de la prueba no se pedirán demostraciones de teoremas.
• Los criterios esenciales de valoración de un ejercicio serán el planteamiento razonado y la ejecución técnica del mismo. La mera descripción del planteamiento sin que se lleve a cabo de manera efectiva no puede ser suficiente para obtener una valoración completa del ejercicio.
• En un ejercicio en el que se pida explícitamente una deducción o justificación razonada, la mera aplicación de una fórmula no será suficiente para obtener una puntuación total.
• Aunque se podrá utilizar calculadoras, todos los procesos conducentes a la obtención de resultados deben estar suficientemente razonados.
• Los errores aritméticos cometidos en un apartado, no se tendrán en cuenta en la calificación de apartados posteriores que puedan verse afectados, siempre que resulten ser de una complejidad equivalente.
• Los errores en las operaciones aritméticas elementales se penalizarán con un máximo del 10 % de la nota total del ejercicio; de igual manera se penalizarán la redacción incorrecta, las faltas de ortografía o el uso incorrecto de símbolos.
• La presentación clara y ordenada se valorará positivamente.
Todas estas normas son las mismas a las que tendrán que someterse los alumnos en las Pruebas de Acceso. De hecho en dicha prueba de los cuatro ejercicios de cada examen (recibirán dos), uno será de Álgebra, otro de Geometría y otros dos de Análisis.

Bienvenidos y ¡ánimo!

   Comenzamos hoy el nuevo curso. La mayoría de vosotros estudiáis 2º de Bachillerato por primera vez y muchos estaréis nerviosos pensando si seréis capaces o no de aprobar todas vuestras asignaturas. Está claro que los estudios que vais a empezar este año no son triviales, muchos contenidos requerirán de vosotros un gran esfuerzo intelectual, e incluso alguno de vosotros, después de haber estudiado, podrá incluso suspender algún examen. Pero el truco consiste en tener una buena motivación y en tener unos buenos hábitos de estudio.

La motivación os servirá para que no os vengáis a bajo en los momentos de mayor tensión, cuando se os acumulen varios exámenes en una semana, o cuando suspendáis algún examen. Cuando esto suceda, lo mejor es analizar que ha pasado, cuales han sido las causas, y buscar las soluciones adecuadas. Las personas inteligentes no son aquellas que nunca se equivocan, sino aquellas que saben resolver todos esos problemas que se nos plantean a diario y que cuando se equivocan, saben levantarse y buscar soluciones.

Los hábitos de estudio son imprescindibles. Algunos de vosotros habrá aprobado cursos de educación secundaria casi sin esfuerzo. A medida que los cursos avanzan, la cosa se complica: los contenidos ya no son triviales, tenéis muchas asignaturas, se os exige nota para entrar en determinadas carreras, habrá semanas en las que tengáis varios exámenes, el temario es el temario del que os examinaréis en Selectividad, … Por todo ello es conveniente que desde el primer día llevéis las asignaturas al día. No vale de nada un atracón los dos últimos días.

También es importante que tengáis vuestros momentos de ocio en los que os liberéis de la tensión. Tan problemático es no tener unos buenos hábitos de estudio como un exceso de responsabilidad. He tenido alumnos que se han derrumbado en la última semana del curso por la tensión que han acumulado.

Mi objetivo es que todos vosotros terminéis aprobando la asignatura, y que lleguéis a disfrutar de las Matemáticas. Espero que alguno de vosotros llegue a apasionarse con un problema, de esos que no se sabe como meterles mano, que llegue a soñar con él, y que un día, os levantéis de la cama a medianoche con el problema resuelto. Esa satisfacción que obtendréis desgraciadamente no podréis compartirla con casi nadie pues pocos os entenderán. Alguno os dirá para que sirve, otros si merecía la pena tanto esfuerzo. Se cuenta que una vez le preguntaron a Edmund Hillary por qué había subido al Everest. Él sólo contestó: “Porqué estaba ahí”.