Diario de clases: Viernes 18 de Septiembre de 2009

INTRODUCCIÓN HISTÓRICA AL ANÁLISIS MATEMÁTICO

Uno de los pilares básicos sobre los que se cimienta el gran edificio de las Matemáticas es el concepto de función. Las funciones, además de ser un importante instrumento dentro de las Matemáticas, también lo son en las demás ciencias: Física, Astronomía, Biología, Economía, Sociología, Medicina, etc.

Cuando iniciamos un estudio en el campo científico, uno de los objetivos es obtener un modelo matemático que nos permita entender y expresar como se relacionan las distintas magnitudes que intervienen. Dicho modelo se debe ajustar a las observaciones o datos empíricos obtenidos.

Se puede afirmar que la culminación del proceso de elaboración del concepto de función es una de las grandes aportaciones de la ciencia en el siglo XVII. Fue un proceso lento que en realidad había comenzado ya en el siglo XIV.

La matemática de la antigüedad fue preponderantemente estática. Es cierto que la geometría de los griegos constituyó una genial exploración racional del espacio, dando origen a una concepción de la matemática y de la ciencia que en esencia es la de hoy, después de veintiséis siglos. Pero la exploración de los diversos tipos de movimientos, la introducción en la matemática de la noción de cambio en el tiempo, la cuantificación de la causalidad en la determinación de un efecto, era algo para lo que la matemática no estuvo suficiente madura, sino después de muchos siglos. De hecho se puede afirmar que durante mucho tiempo el avance en muchos frentes de la ciencia se vio frenado por la incapacidad de la matemática para aportar herramientas adecuadas.

La noción de función surge con fuerza en el campo de la ciencia debido a la generalización del uso del sistema decimal, por la posibilidad de representación y cálculo simbólico de magnitudes heredadas del álgebra y por las posibilidades de medición y observación conseguidas a través de nuevos instrumentos.

Las funciones más interesantes, por supuesto, son las funciones reales de variable real, es decir, aquellas definidas sobre los números reales cuyos valores son también números reales. Su estudio constituye el armazón de toda la matemática actual y, consecuentemente, de toda la ciencia y tecnología modernas. Estas funciones van a constituir el objetivo de este bloque.

En el desarrollo del cálculo infinitesimal, en el siglo XVII, al estudiar la derivada de funciones, la integral,... surgieron problemas relacionados con los procesos infinitos que hubo que introducir, aun sin entenderlos muy bien. Hasta finales del siglo XIX con Weierstrass, no se logró una expresión del cálculo infinitesimal suficientemente rigurosa y correcta. Ello fue posible gracias a la revisión de conceptos básicos como el número real, la noción de límite, la de continuidad, etc.

El antecedente más antiguo que conocemos de lo que hoy se entiende por función se remonta a la época mesopotámica. De este periodo se conservan diversas tablillas de arcilla en las que se recogen series de números relacionados entre sí.

No obstante el estudio de las funciones como relaciones de dependencia entre magnitudes no comenzó a abordarse de forma rigurosa hasta el siglo XVII.

Puede afirmarse que la idea de función está implícita en los trabajos de los matemáticos franceses Rene Descartes y P. de Fermat. Sin embargo hubo de esperar a la publicación en 1638 del Discurso e dimostrazioni matematiché intorno a due nuove scienze, del astrónomo y matemático italiano G. Galilei, para que los modelos funcionales se aplicaran decididamente en las ciencias experimentales, en especial al estudio de las leyes del movimiento.

El análisis es la rama de la matemática que proporciona métodos para la investigación cuantitativa de la dependencia de unas magnitudes respecto de otras, así como de los procesos de cambio que se producen entre ellas.

Esta disciplina surgió de la necesidad de una herramienta que permitiera abordar los problemas que preocupaban a la ciencia del siglo XVII, y que podemos englobar en dos grandes grupos:

El primer grupo incluye problemas físicos, en especial los relacionados con el cálculo de velocidades en un movimiento, junto a problemas geométricos de determinación de tangentes, máximos y mínimos, etc. Este conjunto de problemas condujo a una rama del análisis que recibe el nombre de cálculo diferencial.

El segundo abarca una serie de problemas físicos asociados al cálculo de espacio recorrido en un movimiento, así como problemas geométricos de obtención del área de una figura curvilínea: el llamado problema de la cuadratura. Este conjunto de problemas llevó a otra rama del análisis conocida como cálculo integral.

Reseñas históricas:

- Arquímedes de Siracusa (287- 212 a.C.) utiliza las primeras ideas infinitesimales en el cálculo de áreas.

- Galileo Galilei (1564-1642) estudió el movimiento desde un punto de vista cuantitativo, estableciendo leyes o funciones entre magnitudes.

- John Wallis (1616-1703) utilizó por primera vez en su obra Arithmetica infinitorum el símbolo de "" para representar el infinito.

- Isaac Barrow (1630-1677) preparó el camino para el descubrimiento del cálculo infinitesimal. Estudiaremos el año próximo un famoso teorema que lleva su nombre.

- Gottfried W. Liebnitz (1646-1716) publicó en 1686 en la revista Acta Eruditorum los principios básicos del Cálculo infinitesimal.

- Guillaume Francois Antoine de L'Hopital (1661-1704) publicó en 1696 un tratado de Cálculo diferencial titulado Analyse des infiniment petits, en el que figuraba la famosa regla que lleva su nombre.

- Isaac Newton (1642-1727) en 1693 publicó en su obra De Analysi los principios básicos del Cálculo Infinitesimal. Es considerado junto con Leibniz uno de los padres del Cálculo infinitesimal. La obra más importante de Newton fue Philosophie naturalis principia mathematica (Principios matemáticos de la filosofía natural).

- Leonard Euler (1707-1783) fue uno de los grandes matemáticos que contribuyó a la evolución del Análisis Matemático. Utilizó el símbolo y=f(x) para denotar a una función. En su obra Introductio in analysin infinitorum publicada en 1748 sistematizó los conocimientos de su época y dio una definición de función que presidió en el desarrollo de las matemáticas durante un siglo: "Función es cualquier expresión analítica formada con cantidades variables y con cantidades constantes"

- Bernard Bolzano (1781-1848) matemático checoslovaco muy preocupado por el rigor y la precisión en las demostraciones matemáticas, formuló el teorema que lleva su nombre en 1817.

- Agustín Louis Cauchy (1789-1857) es considerado como el matemático que fundamentó el Cálculo Infinitesimal. La obra fundamental de Cauchy fue Cours D'Analyse de L'Ecole Royale Polytechnique publicada en 1821 en donde cimienta el Cálculo infinitesimal en el concepto de límite.

- Peter Gustav Lejeune Dirichlet (1805-1859) dio la definición rigurosa de función, tal y como la conocemos hoy en día.

- Karl Weierstrass (1815-1897) fue el más destacado fundador de los principios del Análisis y de su rigurosa demostración. A menudo se habla de "rigor weierstrassiano" de una demostración.

- Julio Rey Pastor (1888-1962) ha sido considerado el matemático español más importante del siglo XX.

- Richard Dedekind (1831-1916) y Georg Cantor (1845-1918) demostraron que los números reales llenan o completan la recta, es decir, que a cada punto de la recta le corresponde un número real y viceversa.

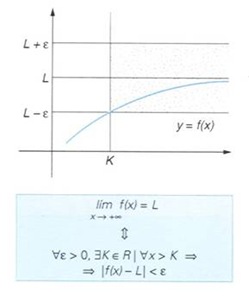
1.- Límite de una función en el infinito

IMPORTANTE: Para completar tu formación, es conveniente que trabajes este recurso

Operaciones con Límites

Si f(x) y g(x) son dos funciones y existen sus límites, se cumple que:

Nota: En todas las expresiones anteriores aparece , queriendo decir que son validas tanto para como para

En el cálculo de límites es necesario operar con expresiones donde aparece infinito. Estas son algunas de las expresiones cuyos resultados son conocidos: