Hoy hemos comenzado con el Bloque III.- Álgebra Lineal.
Hemos definido algunos conceptos importantes:
Definición: Una ecuación lineal es una ecuación polinómica de grado uno con una o varias incógnitas. Diremos que dos ecuaciones son equivalentes cuando tienen la misma solucione ( o soluciones). Si a los dos miembros de una ecuación los multiplicamos o dividimos por un mismo número distinto de cero, la ecuación resultante es equivalente a la primera.
Definición: Un sistema de ecuaciones lineales es un conjunto de ecuaciones lineales dadas conjuntamente con el fin de determinar la o las soluciones comunes a todos ellos. Un sistema con m ecuaciones lineales n incógnitas puede ser escrito en forma ordinaria como:
Donde  son las incógnitas y los números
son las incógnitas y los números 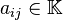 son los coeficientes del sistema sobre el cuerpo
son los coeficientes del sistema sobre el cuerpo ![\mathbb{K}\ [= \R, \mathbb{C}, \dots]](http://upload.wikimedia.org/math/d/d/1/dd172d7f353ca18a891dda59a0d44cc5.png) . En el presente curso los coeficientes serán todos números reales.
. En el presente curso los coeficientes serán todos números reales.
En los sistemas con 2 incógnitas, el universo de nuestro sistema será el plano bidimensional, mientras que cada una de las ecuaciones será representada por una recta, si es lineal. La solución será el punto (o línea) donde intersecten todas las rectas que representan a las ecuaciones. Si no existe ningún punto en el que intersecten al mismo tiempo todas las líneas, el sistema es incompatible, o lo que es lo mismo, no tiene solución.
En el caso de un sistema con 3 incógnitas, el universo será el espacio tridimensional, siendo cada ecuación un plano dentro del mismo. La intersección de dos planos no paralelos es una recta. Si todos los planos intersectan en un único punto, las coordenadas de éste serán la solución al sistema. Si, por el contrario, la intersección de todos ellos es una recta o incluso un plano, el sistema tendrá infinitas soluciones, que serán las coordenadas de los puntos que forman dicha línea o superficie.
Para sistemas de 4 ó más incógnitas, la representación gráfica no es intuitiva para el ser humano, por lo que dichos problemas no suelen enfocarse desde esta óptica.
Tipos de sistemas
Los sistemas de ecuaciones lineales se pueden clasificar según el número de soluciones que pueden presentar. De acuerdo con ese caso se pueden presentar los siguientes casos:
- Sistema incompatible si no tiene ninguna solución.
- Sistema compatible si tiene alguna solución, en este caso además puede distinguirse entre:
- Sistema compatible determinado cuando tiene un número finito de soluciones.
- Sistema compatible indeterminado cuando admite un conjunto infinito de soluciones.
-
Quedando así la clasificación:
Posiciones relativas de dos rectas en el plano





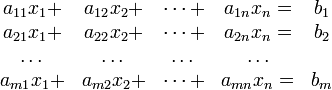

No hay comentarios:
Publicar un comentario